conradcliff
New Member
What I figure is that instead of going by tooth count I can go by outside diameter instead for the ratios.
Now, before I go any further, let me try and explain my setup so that you can have an idea about what I'm planning on. Picture this: My engine is rack mounted, it has a 6 tooth #25 sprocket being driven off of its left side (note: to my knowledge no one makes a #40 sprocket for these bell housings). The chain from the 6 tooth sprocket on the engine runs just forward and slightly down from that to the left side of a jackshaft to a 28 tooth #25 sprocket. On the right side of that jackshaft is a 10 tooth #40 sprocket. A chain runs from this sprocket down and slightly forward to a 44 tooth #40 sprocket. Attached to the same freewheel as the 44 tooth sprocket is a 38 tooth #40 sprocket. This runs back to a 14 tooth gear which is attached to a 26" OD wheel. Basically just picture the SBP setup with a rear mounted 4 stroke engine.
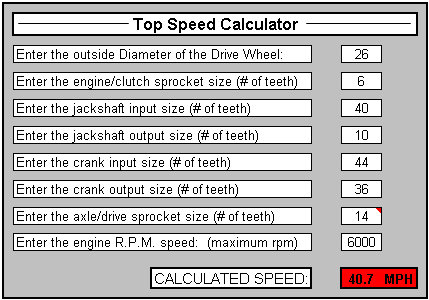
Here are two different versions of basically the same calculations. One uses the tooth counts and one has the outside diameters. (Note: the tooth counts for the #25 sprockets found on the engine and the left side [input side] of the jackshaft have been reduced by about half to mimic the approximate size of the same OD #40 sprockets. A 6 tooth #25 sprocket is approximately equal in outside diameter to a 3 tooth #40 sprocket and a 28 tooth #25 sprocket is approximately equal to a 13.28 tooth #40 sprocket [even though 13.28 tooth sprockets don't actually exist])
As you can see the final calculations are off by a moderate margin.
What I'm aiming for is an approximate speed calculation of 40MPH when I'm shifted into my final gear, which is 14 teeth.
One other difference here is that I had originally shot for 40MPH at 6000RPMs taking into consideration the HP an torque curves of the GXH50 and pocket bike engines. Now that I'm probably going to be utilizing the Titan engine I fear that the max HP and torque range are going to lie within a different RPM range, which would necessitate different calculations entirely..oh well.
So what I really need to know is what size #25 sprocket I need for the input side (left side) of my jackshaft in order to reach 40mph at 6000RPMs...or whatever RPM range you think the Titan has the most power at. And I understand that the Titan may not be able to get me to 40mph..that's ok, I still would like to keep that as the target speed for the given(or optimal if you know it's different for the Titan) RPM range.
Here is a link to the sprocket catalog I got my measurements from.
Here is a link to the ratio calculator I made with the help from the guys at maxtorque. (If you find any problems with it let me know because I just sort of figured it out without any prior knowledge about ratio calculations)
So, I guess that's about that..thanks again for putting up with me and for all the help you guys have provided thus far..hopefully I can get this figured out without having to buy 10 different sprockets to get the right one. :grin5:
P.s. Although I appreciate the concern..let's try to keep the discussion about "40mph being too fast" to a minimum if we can..